在平面直角坐标系
中，已知椭圆
：
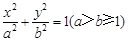的离心率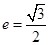
，且椭圆C上一点
到点Q
的距离最大值为4，过点
的直线交椭圆于点
（Ⅰ）求椭圆C的方程；
（Ⅱ）设P为椭圆上一点，且满足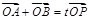
（O为坐标原点），当
时，求实数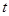
的取值范围.
已知双曲线与椭圆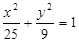
共焦点,它们的离心率之和为
,求双曲线的标准方程。
（本小题满分14分）
已知椭圆C：
＋
＝1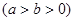
的左．右焦点为
，离心率为
，直线
与x轴、y轴分别交于点
，
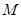是直线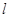
与椭圆C的一个公共点，
是点
关于直线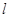的对称点，设
＝
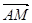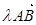
（Ⅰ）证明：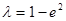
； （Ⅱ）确定
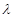的值，使得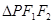
是等腰三角形.
（本小题满分14分）
已知抛物线方程为
，在y轴上截距为2的直线l与抛物线交于M、N两点，O为坐标原点，若OM⊥ON，求直线l的方程．
.（本小题满分12分）
设
是方程x2－ax+b=0的两个实根，试分析a>2且b>1是两根均大于1的什么条件？说明理由.
（本小题10分）
设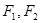
分别为椭圆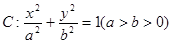
的左、右两个焦点.（1）若椭圆
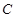上的点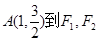
两点的距离之和等于4，求椭圆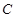的方程和焦点坐标；（2）设点P是（1）中所得椭圆上的动点，
。