已知数列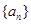 的前
的前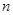 项和为
项和为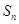 ,常数
,常数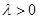 ,且
,且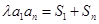 对一切正整数
对一切正整数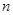 都成立。
都成立。
(Ⅰ)求数列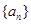 的通项公式;
的通项公式;
(Ⅱ)设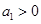 ,
,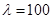 ,当
,当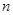 为何值时,数列
为何值时,数列 的前
的前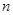 项和最大?
项和最大?
已知 ,点
,点 ,曲线
,曲线 ,若曲线与线段
,若曲线与线段 有两个不同的交点,求实数
有两个不同的交点,求实数 的范围.
的范围.
某人需要补充维生素,现有甲、乙两种维生素胶囊,这两种胶囊都含有维生素 ,
, ,
, ,
, 和最新发现的
和最新发现的 .甲种胶囊每粒含有维生素
.甲种胶囊每粒含有维生素 ,
, ,
, ,
, ,
, 分别是1mg,1mg,4mg,4mg,5mg;乙种胶囊每粒含有维生素
分别是1mg,1mg,4mg,4mg,5mg;乙种胶囊每粒含有维生素 ,
, ,
, ,
, ,
, 分别是3mg,2mg,1mg,3mg,2mg.
分别是3mg,2mg,1mg,3mg,2mg.
如果此人每天摄入维生素 至多19mg,维生素
至多19mg,维生素 至多13mg,维生素
至多13mg,维生素 至多24mg,维生素
至多24mg,维生素 至少12mg,那么他每天应服用两种胶囊多少才能满足维生素的需要量,并能得到最大量的维生素
至少12mg,那么他每天应服用两种胶囊多少才能满足维生素的需要量,并能得到最大量的维生素 .
.
求证:无论 取何值,曲线
取何值,曲线 总通过定点.
总通过定点.
已知曲线上任一点到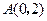 的距离减去它到
的距离减去它到 轴的距离的差是
轴的距离的差是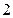 ,求这曲线的方程.
,求这曲线的方程.
两条直线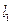 ,
, 分别过点
分别过点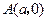 ,
,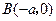 (
(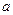 为常数),且分别绕
为常数),且分别绕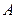 ,
, 旋转,它们分别交
旋转,它们分别交 轴于
轴于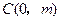 ,
,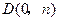 (
( ,
, 为参数),若
为参数),若 ,求两直线交点
,求两直线交点 的轨迹方程.
的轨迹方程.