某人需要补充维生素,现有甲、乙两种维生素胶囊,这两种胶囊都含有维生素 ,
, ,
, ,
, 和最新发现的
和最新发现的 .甲种胶囊每粒含有维生素
.甲种胶囊每粒含有维生素 ,
, ,
, ,
, ,
, 分别是1mg,1mg,4mg,4mg,5mg;乙种胶囊每粒含有维生素
分别是1mg,1mg,4mg,4mg,5mg;乙种胶囊每粒含有维生素 ,
, ,
, ,
, ,
, 分别是3mg,2mg,1mg,3mg,2mg.
分别是3mg,2mg,1mg,3mg,2mg.
如果此人每天摄入维生素 至多19mg,维生素
至多19mg,维生素 至多13mg,维生素
至多13mg,维生素 至多24mg,维生素
至多24mg,维生素 至少12mg,那么他每天应服用两种胶囊多少才能满足维生素的需要量,并能得到最大量的维生素
至少12mg,那么他每天应服用两种胶囊多少才能满足维生素的需要量,并能得到最大量的维生素 .
.
(本小题满分14分)已知在 中,内角
中,内角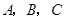 所对边的边长分别是
所对边的边长分别是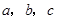 ,若
,若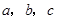 满足
满足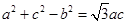
(1)求角B;
(2)若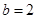 ,∠A=105°,求c边长。
,∠A=105°,求c边长。
(本小题满分12分)求下列不等式的解集:
(1)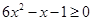 ;
;
(2)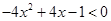
(本小题满分12分)设正项等比数列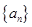 的前
的前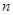 项和为
项和为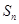 ,已知
,已知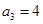 ,
,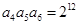 .
.
(1)求首项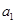 和公比
和公比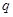 的值;
的值;
(2)若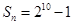 ,求
,求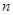 的值
的值
已知函数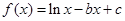 ,
,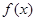 在点
在点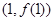 处的切线方程为
处的切线方程为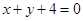 .
.
(Ⅰ)求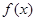 的解析式;
的解析式;
(Ⅱ)求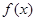 的单调区间;
的单调区间;
(Ⅲ)若在区间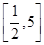 内,恒有
内,恒有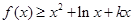 成立,求
成立,求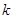 的取值范围.
的取值范围.
(本小题满分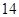 分)如图所示,
分)如图所示,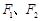 分别为椭圆
分别为椭圆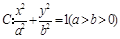 的左、右两个焦点,A、B为两个顶点。已知椭圆C上的点
的左、右两个焦点,A、B为两个顶点。已知椭圆C上的点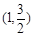 到
到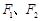 两点的距离之和为4。
两点的距离之和为4。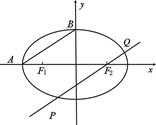
(1)求椭圆C的方程和焦点坐标;
(2)过椭圆C的焦点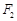 作AB的平行线交椭圆于P、Q两点,求弦PQ的长。
作AB的平行线交椭圆于P、Q两点,求弦PQ的长。