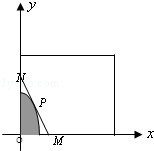
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线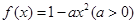 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点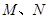 ,交曲线于点
,交曲线于点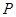 ,设
,设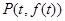 .
.
(1)将△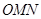 (
(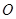 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数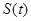 ;
;
(2)若在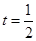 处,
处,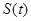 取得最小值,求此时
取得最小值,求此时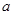 的值及
的值及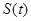 的最小值.
的最小值.
已知向量=(sinA,cosA),=(,-1),·=1,且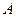 为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
已知=(sinθ,),=(1,),其中θ∈(π,),则一定有()
| A.∥ | B.⊥ | C.与夹角为45° | D.||=|| |
如图,是某市1000户居民月平均用电量的频率分布直方图,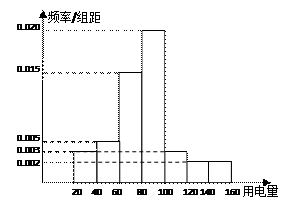
(1)如果当地政府希望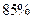 以上的居民每月的用电量不超出标准,这个标准为多少时比较适当?
以上的居民每月的用电量不超出标准,这个标准为多少时比较适当?
(2)计算这1000户居民月用电量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)有关部门为了制定居民月用电量标准,采用分层抽样的方法从1000户居民中抽取50户参加听证会,并且要在这已经确定的50人中随机确定两人做中心发言,求这两人分别来自用电量区间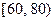 和
和 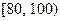 的概率.
的概率.
已知线段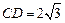 ,
,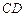 的中点为
的中点为 ,动点
,动点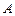 满足
满足 (
(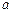 为正常数).
为正常数).
(1)建立适当的直角坐标系,求动点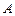 所在的曲线方程;
所在的曲线方程;
(2)若存在点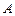 ,使
,使 ,试求
,试求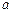 的取值范围;
的取值范围;
(3)若 ,动点
,动点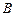 满足
满足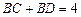 ,且
,且 ,试求
,试求 面积的最大值和最小值.
面积的最大值和最小值.
已知抛物线C: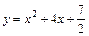 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(1)若C在点M的法线的斜率为 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(2)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.