已知 (a是常数,a∈R)
(a是常数,a∈R)
(Ⅰ)当a=1时求不等式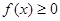 的解集;
的解集;
(Ⅱ)如果函数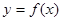 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.
设△ABC三个角A,B,C的对边分别为a,b,c,向量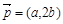 ,
,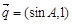 ,且
,且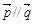 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC是锐角三角形,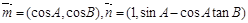 ,求
,求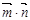 的取值范围.
的取值范围.
已知
已知函数 .
.
(I)求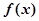 在
在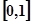 上的最大值;
上的最大值;
(II)若对任意的实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(III)若关于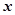 的方程
的方程 在
在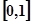 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数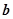 的取值范围.
的取值范围.
如图,矩形ABCD中,AB=CD=2 ,BC=AD=
,BC=AD= 。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
(Ⅰ)求二面角A—BD—C平面角的余弦值。
(Ⅱ)求四面体ABCD外接球的体积; 
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为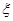 ,求
,求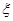 的分布列及数学期望
的分布列及数学期望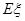 .
.