甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次．记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；
（2）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由；
（3）若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为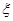
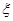，求的分布列及数学期望
.
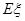已知：A、B是
ABC的两个内角，
，
其中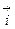
、
为相互垂直的单位矢量．若 | 
| =
，试求tanA·tanB的值．
当m为何实数时，复数z＝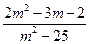
+(m2+3m－10)i；（1）是实数；（2）是虚数；（3）是纯虚数．
抛物线y=ax2＋bx在第一象限内与直线x＋y=4相切．此抛物线与x轴所围成的图形的面积记为S．求使S达到最大值的a、b值，并求Smax．
已知过函数f（x）=
的图象上一点B（1，b）的切线的斜率为－3．
（1）求a、b的值；
（2）求A的取值范围，使不等式f（x）≤A－1987对于x∈[－1，4]恒成立；
令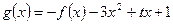
．是否存在一个实数t，使得当
时，g（x）有最大值1？
讨论函数
的单调性，并确定它在该区间上的最大值最小值．