已知数列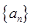 的通项公式为
的通项公式为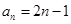 ,数列
,数列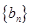 的前
的前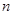 项和为
项和为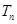 ,且满足
,且满足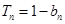 .
.
(1)求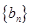 的通项公式;
的通项公式;
(2)在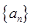 中是否存在使得
中是否存在使得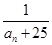 是
是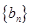 中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且 .
.
(1)求证:EF∥平面BDC1;
(2)求证: 平面
平面 .
.
在△ABC中,内角A,B,C的对边分别为a,b,c,若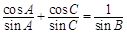 .
.
(1)求证: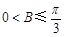 ;
;
(2)若 ,且
,且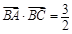 ,求
,求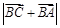 的值.
的值.
(1)已知 ,求证:
,求证: ;
;
(2)已知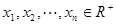 ,且
,且 ,
,
求证: .
.
某超市在节日期间进行有奖促销,规定凡在该超市购物满400元的顾客,均可获得一次摸奖机会.摸奖规则如下:
奖盒中放有除颜色不同外其余完全相同的4个球(红、黄、黑、白).顾客不放回的每次摸出1个球,若摸到黑球则摸奖停止,否则就继续摸球.按规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次摸奖停止的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布列和数学期望.
的分布列和数学期望.