某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:


参考公式:线性回归方程系数: ,
, )
)
已知函数
.
(1)试讨论
的单调性;
(2)若
(实数
是
与无关的常数),当函数
有三个不同的零点时,
的取值范围恰好是
,求
的值.
如图,在平面直角坐标系
中,已知椭圆
的离心率为
,且右焦点
到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过
的直线与椭圆交于
两点,线段
的垂直平分线分别交直线
和
于点
,若
,求直线
的方程.
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为
,山区边界曲线为
,计划修建的公路为l,如图所示,
,
为
的两个端点,测得点
到
的距离分别为5千米和40千米,点
到
的距离分别为20千米和2.5千米,以
所在的直线分别为
,
轴,建立平面直角坐标系
,假设曲线
符合函数
(其中
,
为常数)模型.
(1)求
,
的值;
(2)设公路l与曲线
相切于
点,
的横坐标为
.
①请写出公路l长度的函数解析式
,并写出其定义域;
②当
为何值时,公路l的长度最短?求出最短长度.
如图,在直三棱柱
中,已知
,设
的中点为
,
.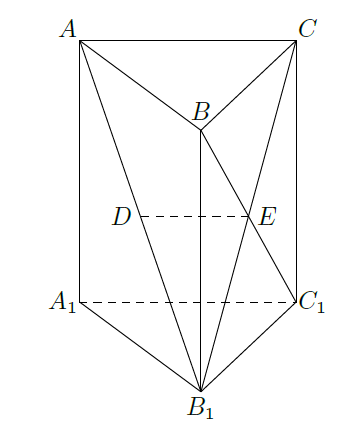
求证:
(1) 平面
(2) .
在
中,已知
.
(1)求
的长;
(2)求
的值.