如图所示的电路中,两平行金属板A、B水平放置,两板间的距离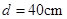 ,电源电动势
,电源电动势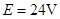 ,内电阻
,内电阻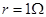 ,电阻
,电阻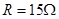 ,闭合开关S,待电路稳定后,一带电量
,闭合开关S,待电路稳定后,一带电量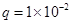 C, 质量
C, 质量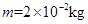 的小球恰好静止于两板之间。取
的小球恰好静止于两板之间。取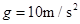 ,求:
,求: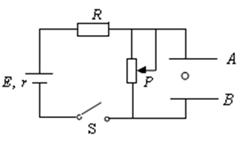
(1)两板间的电压为多少
(2)此时,滑动变阻器接入电路的阻值为多少
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d="40" cm.电源电动势E="24" V,内电阻r="1" Ω,电阻R="15" Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间.若小球带电量为q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力.那么,滑动变阻器接入电路的阻值为多大时,小球恰能到达A板?此时,电源的输出功率是多大?(取g="10" m/s2)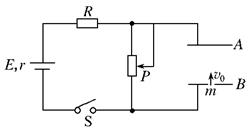
如图所示的电路中,电源的电动势E="3.0" V,内阻r="1.0" Ω;电阻R1="10" Ω,R2="10" Ω,R3="30" Ω,R4="35" Ω;电容器的电容C="100" μF.电容器原来不带电.求接通电键S后流过R4的总电荷量.
如图所示,电源电动势E="4.0" V,电源内电阻r="0.50" Ω,电阻器R2="18" Ω,安培表A1的读数为0.50 A,安培表A2的读数为0.30 A,伏特表V的读数为3.0 V,求:R1、R3、R4的阻值各多大?(不计各电表内阻的影响)
图甲是一种家用电熨斗的电路原理图(额定电压为220 V).R0是定值电阻,R是可变电阻(调温开关),其电阻值均不受温度影响.
(1)该电熨斗温度最低时的耗电功率为121 W,温度最高时的耗电功率为484 W,求R0的阻值及R的阻值变化范围.
(2)假定电熨斗每秒钟散发的热量q跟电熨斗表面温度与环境温度的温差关系如图乙所示,现在温度为20 ℃的房间使用该电熨斗来熨烫毛料西服,要求熨斗表面温度为220 ℃,且保持不变,问应将R的阻值调为多大?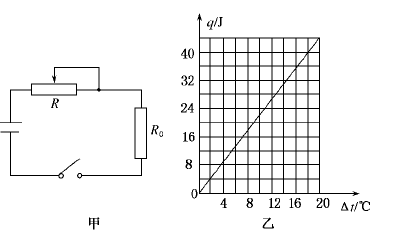
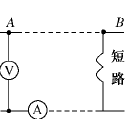
在相距40 km的A、B两地架两条输电线,电阻共为800 Ω,如果在A、B间的某处发生短路,这时接在A处的电压表示数为10 V,电流表示数为40 mA,求发生短路处距A有多远?如图所示.