(本小题12分)在甲、乙两个盒子中分别装有标号为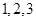 的三个大小相同的球,现从甲、乙两个盒子中各取出
的三个大小相同的球,现从甲、乙两个盒子中各取出 个球,每个球被取出的可能性相等.
个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之和不小于 的概率.
的概率.
(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
| 甲 |
82 |
82 |
79 |
95 |
87 |
| 乙 |
95 |
75 |
80 |
90 |
85 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
(本小题12分)命题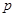 :关于
:关于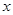 的不等式
的不等式 对于一切
对于一切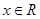 恒成立,命题
恒成立,命题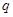 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数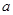 的取值范围;
的取值范围;
(本小题10分)某种产品的广告费用支出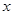 与销售额
与销售额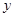 之间有如下的对应数据:
之间有如下的对应数据:
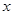 |
2 |
4 |
5 |
6 |
8 |
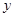 |
30 |
40 |
50 |
60 |
70 |
(1)求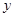 对
对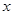 的回归直线方程;
的回归直线方程;
(2)据此估计广告费用为10销售收入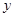 的值.
的值.
参考公式: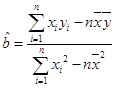
(本小题满分12分)
已知偶函数 的定义域为
的定义域为 ,且在
,且在 上是增函数.
上是增函数.
(Ⅰ)试比较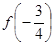 与
与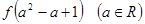 的大小;
的大小;
(Ⅱ)若 ,求不等式
,求不等式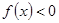 的解集.
的解集.