某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为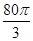 立方米,且
立方米,且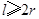 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为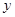 千元.
千元.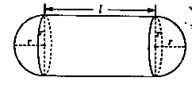
(Ⅰ)写出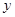 关于
关于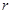 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的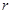 .
.
已知函数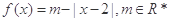 ,且
,且 的解集为
的解集为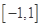 .
.
(1)求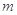 的值;
的值;
(2)若 ,且
,且 ,求证:
,求证: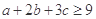 .
.
已知曲线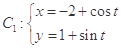 (t为参数),
(t为参数), (
(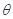 为参数).
为参数).
(1)化 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)过曲线 的左顶点且倾斜角为
的左顶点且倾斜角为 的直线
的直线 交曲线
交曲线 于
于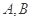 两点,求
两点,求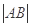 .
.
直线AB经过⊙O上的点C,并且OA=OB,CA=CB.⊙O交直线OB于E,D,连接EC,CD.
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=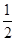 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
已知函数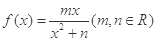 在
在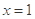 处取得极值
处取得极值 .
.
(1)求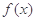 的表达式;
的表达式;
(2)设函数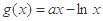 .若对于任意的
.若对于任意的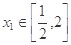 ,总存在唯一的
,总存在唯一的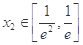 ,使得
,使得 ,求实数
,求实数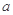 的取值范围.
的取值范围.
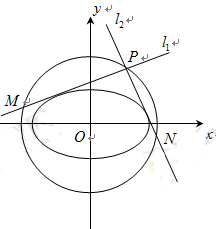
给定椭圆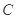 :
: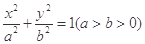 ,称圆心在原点
,称圆心在原点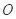 ,半径为
,半径为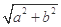 的圆是椭圆
的圆是椭圆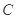 的“准圆”.若椭圆
的“准圆”.若椭圆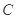 的一个焦点为
的一个焦点为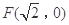 ,其短轴上的一个端点到
,其短轴上的一个端点到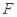 的距离为
的距离为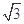 .
.
(1)求椭圆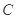 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点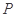 是椭圆
是椭圆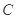 的“准圆”上的动点,过点
的“准圆”上的动点,过点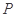 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点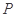 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段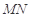 的长为定值.
的长为定值.