(选修4-2:矩阵与变换) 已知矩阵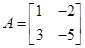 , (1)求逆矩阵
, (1)求逆矩阵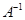 ;(2)若矩阵
;(2)若矩阵 满足
满足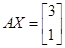 ,试求矩阵
,试求矩阵 .
.
已知圆C1的方程为 动圆C与圆C1、C2相外切。
动圆C与圆C1、C2相外切。
(I)求动圆C圆心轨迹E的方程;
(II)若直线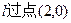 且与轨迹E交于P、Q两点。
且与轨迹E交于P、Q两点。
①设点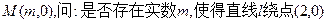 无论怎样转动,都有
无论怎样转动,都有 成立?若存在,求出实数m的值;若不存在,请说明理由;
成立?若存在,求出实数m的值;若不存在,请说明理由;
②过P、Q作直线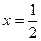 的垂线PA、QB,垂足分别为A、B,记
的垂线PA、QB,垂足分别为A、B,记 的取值范围。
的取值范围。
设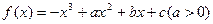 ,在
,在 处取得极大值,且存在斜率为
处取得极大值,且存在斜率为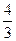 的切线。
的切线。
(1)求 的取值范围;
的取值范围;
(2)若函数 在区间
在区间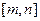 上单调递增,求
上单调递增,求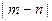 的取值范围;
的取值范围;
(3)是否存在 的取值使得对于任意
的取值使得对于任意 ,都有
,都有 。
。
如图,四棱锥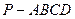 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,
,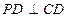 ,
,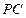 与底面
与底面 所成的角的正切值为
所成的角的正切值为 ,
,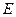 为
为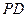 中点.
中点.
(1) 求二面角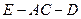 的大小.
的大小.
(2) 在线段 上是否存在点
上是否存在点 ,使得点
,使得点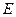 到平面
到平面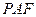 的距离为
的距离为 .若存在,确定点
.若存在,确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
已知数列
 (1)若
(1)若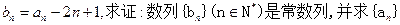 的通项;
的通项;
(2)若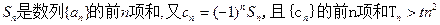 在
在 时恒成立,求实数t的取值范围。
时恒成立,求实数t的取值范围。
先后2次抛掷一枚骰子,将得到的点数分别记为 .
.
(1)求直线 与圆
与圆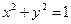 相切的概率;
相切的概率;
(2)将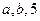 的值分别作为三条线段的长,试列举出这三条线段能围成等腰三角形的所有情形并求其概率.
的值分别作为三条线段的长,试列举出这三条线段能围成等腰三角形的所有情形并求其概率.