已知点(1, )是函数
)是函数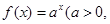 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列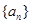 的前
的前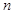 项和为
项和为 ,数列
,数列
 的首项为
的首项为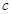 ,且前
,且前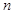 项和
项和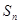 满足
满足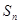 -
- =
=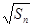 +
+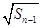 (
(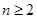 ).
).
(1)求数列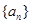 和
和 的通项公式;
的通项公式;
(2)求数列{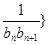 前
前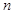 项和为
项和为 ,问
,问 >
>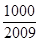 的最小正整数
的最小正整数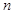 是多少?
是多少?
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.
(Ⅰ)根据茎叶图判断哪个班的平均身高较高;
(Ⅱ)现从乙班这1 0名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
0名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
已知数列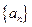 的各项均为正数,观察下面程序框图,
的各项均为正数,观察下面程序框图,
(1)分别写出当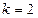 ;
;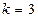 时,
时,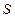 的表达式。
的表达式。
(2)当输入 时,有
时,有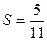 ,求数列
,求数列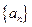 的通项公式
的通项公式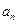 ;
;
(3)在(2)的条件下,若令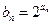 ,求
,求 的
的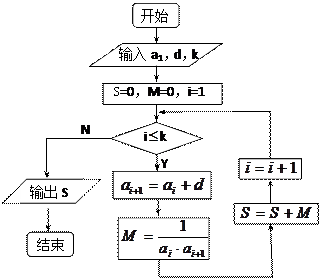
根据下列算法按要求分别完成下列问题,其中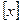 表示不超过
表示不超过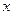 的最大整数。
的最大整数。
(1)此算法的功能是
(2)输出的S值为
(3)根据此算法完成方框内的流程图
下面的茎叶图是某班在一次测验时的成绩,程序用同时统计女生、男生及全班成绩的平均分,试回答下列问题:
(1) 在程序中,“=0”的含义是什么?
横线①处应填什么?
(2) 执行程序,输出S,T,A的值分别是多少?
(3) 请分析该班男女生的习情况.
 已知数列
已知数列 中,
中, ,且
,且
 ,求这个数列的第m项
,求这个数列的第m项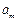 的值
的值 .现给出此算法流程图的一部分如图1,
.现给出此算法流程图的一部分如图1,
(1)请将空格部分(两个)填上适当的内容;
(2)用“For”循环语句写出对应的算法;
(3)若输出S=16,则输入的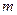 的值是多少?
的值是多少?