(本小题满分12分)在平面直角坐标系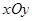 中,点
中,点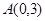 ,直线
,直线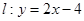 ,设圆
,设圆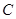 的半径为
的半径为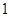 ,圆心在
,圆心在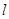 上.
上.
(1)若圆心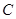 也在直线
也在直线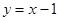 上,过点
上,过点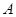 作圆
作圆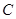 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆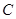 上存在点
上存在点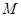 ,使
,使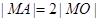 ,求圆心
,求圆心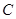 的横坐标
的横坐标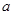 的取值范围.
的取值范围.
已知:以点C(t,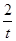 ) (
) ( )为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为坐标原点。
)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为坐标原点。
(1)求证: 的面积为定值。
的面积为定值。
(2)设直线 与圆C交于点M、N,若OM=ON,求圆C的方程。
与圆C交于点M、N,若OM=ON,求圆C的方程。
已知圆C过点A(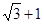 ,0)、B(
,0)、B(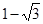 ,0),半径为2,且圆心在X轴上方。
,0),半径为2,且圆心在X轴上方。
(1)求圆C的方程
(2)求圆C关于直线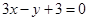 对称的圆的方程。
对称的圆的方程。
如图,四棱锥S—ABCD的底面为正方形,SD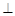 底面ABCD,则下列结论中不正确的是()
底面ABCD,则下列结论中不正确的是()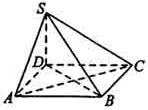
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60), ,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: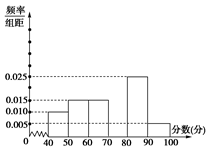
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
两人约定在20∶00到21∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20∶00至21∶00各时刻相见的可能性是相等的,求两人在约定时间内相见的概率。