已知：以点C（t,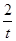
） （
）为圆心的圆与x轴交于点O、A，与y轴交于点O、B，其中O为坐标原点。
（1）求证：
的面积为定值。
（2）设直线
与圆C交于点M、N，若OM=ON，求圆C的方程。
（本小题满分12分）
函数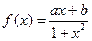
是定义域在（－1，1）上的奇函数，且
.
（1）确定函数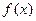
的解析式；
（2）用定义证明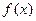在（－1，1）上是增函数；
（3）解不等式
.
（本小题满分12分）
如图，ABCD是正方形，O是正方形的中心，PO
底面ABCD，E是PC的中点．
求证：（1）PA∥平面BDE；
（2）平面PAC平面BDE．
（本小题满分12分）
如图，在棱长为1的正方体ABCD-A1B1C1D1中.
（1）求证：AC⊥平面B1BDD1；
（2）求三棱锥B-ACB1体积．
（本小题满分12分）
已知函数
.
（1）当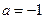
时，求函数的最大值和最小值；
（2）求实数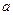
的取值范围，使
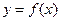在区间
上是单调函数
（本小题满分12分）
一个几何体的三视图如图所示，已知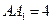
，
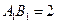,俯视图是一个正三角形.
（1）画出这个几何体的直观图（不要求写画法）；
（2）求这个几何体的表面积及体积.