已知 均在椭圆
均在椭圆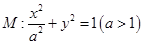 上,直线
上,直线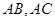 分别过椭圆的左、右焦点
分别过椭圆的左、右焦点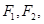 当
当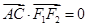 时,有
时,有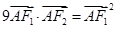
(1)求椭圆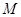 的方程
的方程
(2)设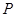 是椭圆
是椭圆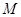 上的任一点,
上的任一点,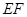 为圆
为圆 的任一条直径,求
的任一条直径,求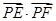 的最大值
的最大值
如图,在三棱锥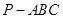 中,
中, 底面
底面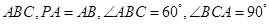 ,点
,点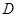 ,
,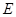 分别在棱
分别在棱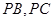 上,且
上,且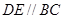
(Ⅰ)求证: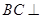 平面
平面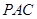 ;
;
(Ⅱ)当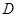 为
为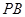 的中点时,求
的中点时,求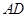 与平面
与平面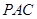 所成的角的正弦;
所成的角的正弦;
(Ⅲ)是否存在点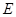 使得二面角
使得二面角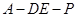 为直二面角?并说明理由.
为直二面角?并说明理由.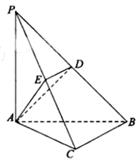
已知数列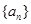 的首项
的首项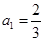 ,
,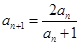 ,
,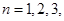 ….
….
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)求数列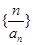 的前
的前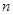 项和
项和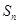 .
.
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| 文艺节目 |
新闻节目 |
总计 |
|
| 20至40岁 |
40 |
10 |
50 |
| 大于40岁 |
20 |
30 |
50 |
| 总计 |
60 |
40 |
100 |
(1)由表中数据检验,有没有99.9%把握认为收看文艺节目的观众与年龄有关?
(2)20至40岁,大于40岁中各抽取1名观众,求两人恰好都收看文艺节目的概率.
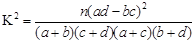
| P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
在 中,角
中,角 所对的边分别为
所对的边分别为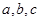 且满足
且满足
(I)求角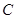 的大小;
的大小;
(II)求函数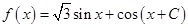
 的最大值,并求取得最大值时
的最大值,并求取得最大值时 的大小.
的大小.