某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：

	文艺节目	新闻节目	总计
20至40岁	40	10	50
大于40岁	20	30	50
总计	60	40	100

（1）由表中数据检验，有没有99.9%把握认为收看文艺节目的观众与年龄有关？
（2）20至40岁，大于40岁中各抽取1名观众，求两人恰好都收看文艺节目的概率．
　

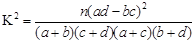
P(k^2>k)	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.84	5.024	6.635	7.879	10.83

科目 数学   题型 解答题   难度 容易