某出版社新出版一本高考复习用书，该书的成本为5元/本，经销过程中每本书需付给代理商m元（1≤m≤3）的劳务费，经出版社研究决定，新书投放市场后定价为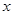
元/本（9≤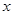≤11），预计一年的销售量为
万本．
(1)求该出版社一年的利润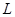
（万元）与每本书的定价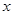的函数关系式；
(2)当每本书的定价为多少元时，该出版社一年的利润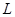最大,并求出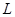的最大值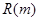
．
某人随机地将编号为1，2，3，4的四个小球放入编号为1，2，3，4的四个盒子中，每个盒子放一个小球，全部放完。
（I）求编号为奇数的小球放入到编号为奇数的盒子中的概率值；
（II）当一个小球放到其中一个盒子时， 若球的编号与盒子的编号相同 ，称这球是“放对”的，否则称这球是“放错”的。设“放对”的球的个数为
的分布列及数学期望。
已知
是数列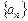
的前n项和，满足关系式
，
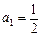
（n≥2，n为正整数）.
（1）令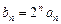
，证明：数列
是等差数列；
（2）求数列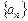的通项公式；
（3）对于数列
，若存在常数M＞0，对任意的
，恒有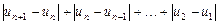
≤M成立，称数列为“差绝对和有界数列”，
证明：数列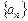为“差绝对和有界数列”.
设m为实数，函数
，
.
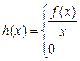
（1）若
≥4，求m的取值范围；
（2）当m＞0时，求证
在
上是单调递增函数；
（3）若对于一切
，不等式≥1恒成立，求实数m的取值范围.
某学校数学兴趣小组有10名学生，其中有4名女同学；英语兴趣小组有5名学生，其中有3名女学生，现采用分层抽样方法（层内采用不放回简单随机抽样）从数学兴趣小组、英语兴趣小组中共抽取3名学生参加科技节活动。
（1）求从数学兴趣小组、英语兴趣小组各抽取的人数；
（2）求从数学兴趣小组抽取的学生中恰有1名女学生的概率；
（3）记
表示抽取的3名学生中男学生数，求的分布列及数学期望。
如图，过椭圆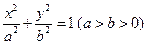
的左焦点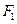
作x轴的垂线交椭圆于点P，点A和点B分别为椭圆的右顶点和上顶点，OP∥AB．
（1）求椭圆的离心率e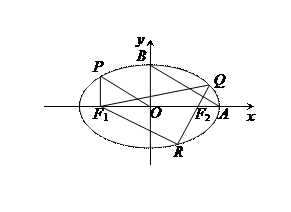
（2）过右焦点
作一条弦QR，使QR⊥AB．若△
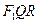的面积为
，求椭圆的方程．