(本小题满分12分)
如图,在某点B处测得建筑物AE的顶端A的仰角为 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2 ,再继续前进10
,再继续前进10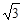 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4 ,求建筑物AE的高度。
,求建筑物AE的高度。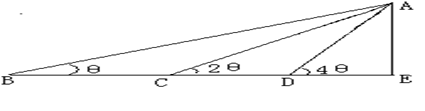
(本小题满分12分)
在△ABC中, 是角
是角 所对的边,且
所对的边,且 .
.
(1)求角 的大小;(2)若
的大小;(2)若 ,求△ABC周长的最大值。
,求△ABC周长的最大值。
(21) (本小题满分15分)
直线 分抛物线
分抛物线 与
与 轴所围成图形为面积相等的两个部分,求
轴所围成图形为面积相等的两个部分,求 的值.
的值.
(本小题满分15分)(文)如图,在四棱锥P-ABCD中,底面为直角梯形,AD//BC, BAD=
BAD= ,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ) 求CD与平面ADMN所成角的余弦
(本小题满分14分)
已知函数 其中实数
其中实数 。
。
(1)若a=-2,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在x=1处取得极值,试讨论
在x=1处取得极值,试讨论 的单调性。
的单调性。