新晨投资公司拟投资开发某项新产品,市场评估能获得 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
.
(1)设奖励方案的函数模型为 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 的基本要求.
的基本要求.
(2)下面是公司预设的两个奖励方案的函数模型:
① ; ②
; ②
试分别分析这两个函数模型是否符合公司要求.
以坐标原点O为极点, 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为: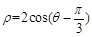 ,曲线C2的参数方程为:
,曲线C2的参数方程为: ,点N的极坐标为
,点N的极坐标为 .
.
(Ⅰ)若M是曲线C1上的动点,求M到定点N的距离的最小值;
(Ⅱ)若曲线C1与曲线C2有有两个不同交点,求正数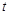 的取值范围.
的取值范围.
如图,已知圆⊙O1与圆⊙O2外切于点P,过点P的直线交圆⊙O1于A,交圆⊙O2于B,AC为圆⊙O1直径,BD与⊙O2相切于B,交AC延长线于D.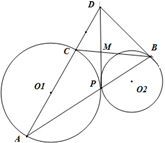
(Ⅰ)求证: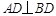
(Ⅱ)若BC、PD相交于点M,则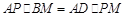
已知函数 .
.
(Ⅰ)若函数在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;
(Ⅱ)如果当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围,并且判断代数式
的取值范围,并且判断代数式 的大小.
的大小.
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且
(Ⅰ)写出年利润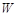 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大
已知直角梯形 ,
, 是
是 边上的中点(如图甲),
边上的中点(如图甲), ,
, ,
,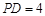 ,将
,将 沿
沿 折到
折到 的位置,使
的位置,使 ,点
,点 在
在 上,且
上,且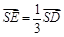 (如图乙)
(如图乙)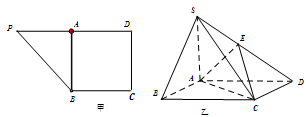
(Ⅰ)求证: 平面ABCD.
平面ABCD.
(Ⅱ)求二面角E−AC−D的余弦值