(本小题满分16分) 对于项数为 的有穷数列
的有穷数列 ,记
,记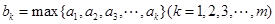 ,即
,即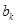 为
为 中的最大值,则称
中的最大值,则称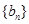 是
是 的“控制数列”,
的“控制数列”,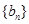 各项中不同数值的个数称为
各项中不同数值的个数称为 的“控制阶数”.
的“控制阶数”.
(Ⅰ)若各项均为正整数的数列 的控制数列
的控制数列 为
为 ,写出所有的
,写出所有的 ;
;
(Ⅱ)若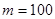 ,
, ,其中
,其中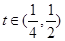 ,
,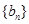 是
是 的控制数列,试用
的控制数列,试用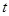 表示
表示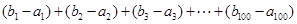 的值;
的值;
(Ⅲ)在 的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
(本小题满分12分)在几何体ABCDE中,∠BAC=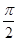 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1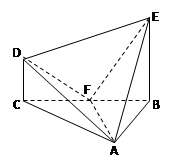
(Ⅰ)求证:DC∥平面ABE;
(Ⅱ)求证:AF⊥平面BCDE;
(Ⅲ)求证:平面AFD⊥平面AFE.
(本小题满分12分)在 中,设内角A,B,C的对边分别为
中,设内角A,B,C的对边分别为 ,向量
,向量 ,若
,若
(1)求角的大小;
(2)若 且
且 ,求
,求 的面积.
的面积.
(本小题满分12分)已知等比数列 满足
满足 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, ,求数列
,求数列 的前
的前 项和
项和 。
。
(本小题满分12分)已知函数
 。
。
(1)求函数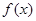 的最小正周期;
的最小正周期;
(2)求函数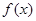 的单调递增区间,并写出对称轴方程.
的单调递增区间,并写出对称轴方程.
(本小题满分14分)
选修4-2:矩阵及其变换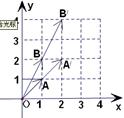
(1)如图,向量 被矩阵M作用后分别变成
被矩阵M作用后分别变成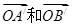 ,
,
(Ⅰ)求矩阵M;
(Ⅱ)并求 在M作用后的函数解析式;
在M作用后的函数解析式;
选修4-4:坐标系与参数方程
( 2)在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为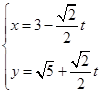 (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点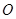 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为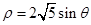 。
。
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设圆 与直线
与直线 交于点
交于点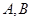 。若点
。若点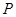 的坐标为(3,
的坐标为(3,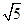 ),求
),求 。
。
选修4-5:不等式选讲
(3)已知 为正实数,且
为正实数,且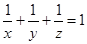 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.