(本小题满分12分)在 中,设内角A,B,C的对边分别为
中,设内角A,B,C的对边分别为 ,向量
,向量 ,若
,若
(1)求角的大小;
(2)若 且
且 ,求
,求 的面积.
的面积.
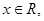 则
则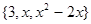 中的元素
中的元素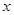 应满足什么条件?
应满足什么条件?
(本小题满分14分)(理科)已知椭圆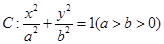 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点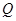
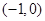 的直线
的直线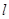 交椭圆于
交椭圆于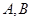 两点,交直线
两点,交直线 于点
于点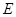 ,且
,且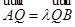 ,
,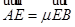 ,
,
求证: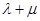 为定值,并计算出该定值.
为定值,并计算出该定值.
(本小题满分14分)(文科)已知曲线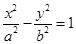
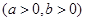 的离心率
的离心率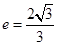 ,直线
,直线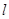 过
过 、
、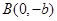 两点,原点
两点,原点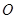 到
到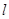 的距离是
的距离是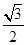 .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点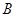 作直线
作直线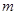 交双曲线于
交双曲线于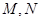 两点,若
两点,若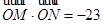 ,求直线
,求直线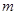 的方程.
的方程.
(本小题满分13分) 已知抛物线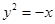 与直线
与直线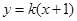 相交于
相交于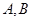 两点.
两点.
(1)求证:以 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点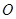 ;(2)当
;(2)当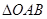 的面积等于
的面积等于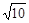 时,求
时,求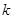 的值.
的值.
(本小题满分12分)已知抛物线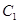 :
: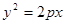 的准线经过双曲线
的准线经过双曲线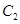 :
: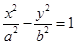 的左焦点,若抛物线
的左焦点,若抛物线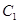 与双曲线
与双曲线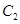 的一个交点是
的一个交点是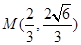 .
.
(1)求抛物线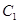 的方程; (2)求双曲线
的方程; (2)求双曲线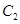 的方程.
的方程.