设抛物线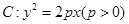 的焦点为
的焦点为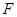 ,准线为
,准线为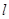 ,
, ,以
,以 为圆心的圆
为圆心的圆 与
与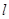 相切于点
相切于点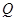 ,
,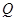 的纵坐标为
的纵坐标为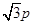 ,
, 是圆
是圆 与
与 轴除
轴除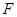 外的另一个交点.
外的另一个交点.
(I)求抛物线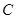 与圆
与圆 的方程;
的方程;
(II)过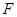 且斜率为
且斜率为 的直线
的直线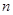 与
与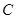 交于
交于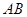 两点,求
两点,求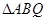 的面积.
的面积.
已知抛物线 .
.
(1)若直线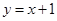 与抛物线
与抛物线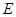 相交于
相交于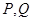 两点,求
两点,求 弦长;
弦长;
(2)已知△ 的三个顶点在抛物线
的三个顶点在抛物线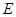 上运动.若点
上运动.若点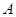 在坐标原点,
在坐标原点,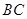 边过定点
边过定点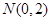 ,点
,点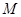 在
在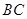 上且
上且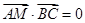 ,求点
,求点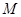 的轨迹方程.
的轨迹方程.
已知复数 满足:
满足: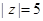 且
且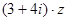 是纯虚数,求复数
是纯虚数,求复数 .
.
已知函数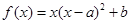 在
在 处有极大值.
处有极大值.
(Ⅰ)求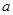 的值;
的值;
(Ⅱ)若过原点有三条直线与曲线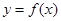 相切,求
相切,求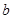 的取值范围;
的取值范围;
(Ⅲ)当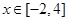 时,函数
时,函数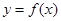 的图象在抛物线
的图象在抛物线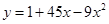 的下方,求
的下方,求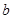 的取值范围.
的取值范围.
在直角坐标系xOy中,直线l的方程为x-y+4=0,
曲线C的参数方程为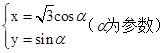 .
.
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,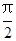 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值.
(Ⅲ)请问是否存在直线m , m∥l且m与曲线C的交点A、B满足 ;
;
若存在请求出满足题意的所有直线方程,若不存在请说明理由。
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含 个小正方形.
个小正方形.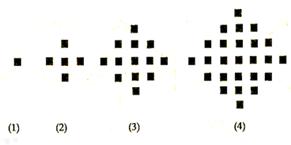
(Ⅰ)求出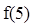 ;
;
(Ⅱ)利用合情推理的“归纳推理思想”归纳出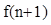 与
与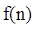 的关系式,
的关系式,
(Ⅲ)根据你得到的关系式求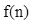 的表达式.
的表达式.