（1）、动手操作：
如图①：将矩形纸片ABCD折叠，使点D与点B重合，点C落在点
处，折痕为EF，若∠ABE＝20°，那么
的度数为 .
（2）、观察发现：
小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．
（3）、实践与运用：
将矩形纸片ABCD按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP＝MN＝PQ（如图④），求∠MNF的大小.
抛物线y=-x2+（m-1）x+m与y轴交于（0，3）点．
（1）求出m的值并在图中画出这条抛物线．
（2）求它与x轴的交点和抛物线顶点的坐标．
（3）x取值什么值时，抛物线在x轴上方？
（4）x取什么值时，y的值随x的增大而减小？
某住宅小区的物业管理部门为解决住户停车困难，将一条道路辟为停车场，停车位置如图所示。已知矩形ABCD是供一辆机动车停放的车位，其中AB=5.4米，BC=2.2米，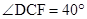
。请计算停车位所占道路的宽度EF（结果精确到0.1米）。
参考数据：sin40°≈0.64 cos40°≈0.77 tan40°≈0.84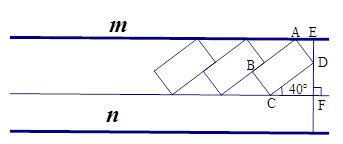 
解不等式组：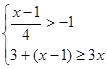
；并将解集在数轴上表示出来．
先阅读下列知识，然后解答下面两个问题：
含有一个未知数，并且未知数的最高次指数是2的方程，叫做一元二次方程，如：
.
我们把它的一般形式记作：
(a、b、c表示已知量，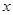
是未知数，a≠0)，它的解的情况是：
① 当
时，方程有两个不相等的解；
② 当
时，方程有两个相等的解（即一个解）；
③ 当
时，方程没有解；
（1）一元二次方程
有几个解？为什么？
（2）当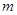
取何值时，关于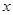的一元二次方程
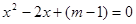没有解？
数学兴趣小组到外旅游拍一张合影，冲一张底片需1.6元，洗一张照片需0.55元。若每人都得到一张照片，那么平均每人分摊的钱不超过0.7元，问这个小组至少有多少人？