甲车在弯路做刹车试验,收集到的数据如下表所示:
速度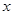 (千米/时) (千米/时) |
0 |
5 |
10 |
15 |
20 |
25 |
… |
刹车距离 (米) (米) |
0 |
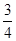 |
2 |
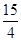 |
6 |
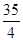 |
… |
(1)请用上表中的各对数据 作为点的坐标,在如图所示的坐标系中画出刹车距离
作为点的坐标,在如图所示的坐标系中画出刹车距离 (米)与速度
(米)与速度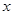 (千米/时)的函数图象,并求函数的解析式;
(千米/时)的函数图象,并求函数的解析式;
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向而行,同时刹车,但还是相撞了.事后测得甲、乙两车刹车距离分别为12米和10.5米,又知乙车刹车距离 (米)与速度
(米)与速度 (千米/时)满足函数
(千米/时)满足函数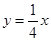 ,请你就两车速度方面分析相撞原因.
,请你就两车速度方面分析相撞原因.
如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派
三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是
直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑300米到离B点最近的D
点,再跳入海中。救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒。
若∠BAD=45°,∠BCD=60°,三名救生员同时从A点出发,请说明谁先到达营救地点B。
(参考数据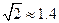 ,
,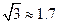 )
)
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交
叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东
30°方向上,AB=2km,∠DAC=15°。
(1)求B、D之间的距离;
(2)求C、D之间的距离。 
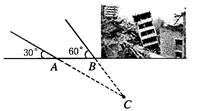
某地震救援队探测出某建筑物废墟下方点 C 处有生命迹象,已知废墟一侧地面上两探
测点A、B 相距 3 米,探测线与地面的夹角分别是30°和 60°(如图),试确定生命
所在点 C 的深度.(结果精确到0.1米,参考数据: )
)
梯形ABCD是拦水坝的横断面图,(图中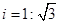 是指坡面的铅直高度DE与水平宽度CE
是指坡面的铅直高度DE与水平宽度CE
的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积。(结果保留三位有效
数字,参考数据: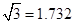 ,
,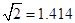 )
)
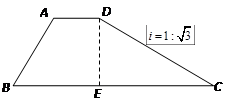 |
阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,
顶部不易到达),他们带了以下测量工具:皮尺、标杆、一副三角尺、小平面镜。请你
在他们提供的测量工具中选出所需工具,设计一种测量方案。
(1)所需的测量工具是:;
(2)请在下图中画出测量示意图;
(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x。
 |