(本小题共13分)
已知函数 ,且
,且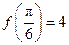 .
.
(Ⅰ)求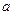 的值;
的值;
(Ⅱ)当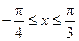 时,求函数
时,求函数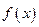 的值域.
的值域.
(本小题14分)已知数列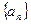 为等差数列,
为等差数列,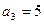 ,
,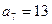 ,数列
,数列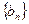 的前
的前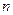 项和为
项和为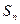 ,且有
,且有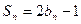
(1)求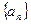 、
、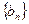 的通项公式;
的通项公式;
(2)若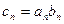 ,
,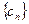 的前
的前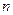 项和为
项和为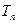 ,求
,求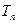 ;
;
(3)试比较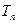 与
与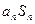 的大小,并说明理由.
的大小,并说明理由.
.(本小题14分)椭圆
 的一个顶点为
的一个顶点为
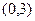 ,离心率
,离心率
(1)求椭圆方程;
(2)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点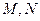 ,且满足
,且满足 ,
, ,求直线
,求直线 的方程.
的方程.
(本小题14分)已知函数 .
.
(1)若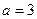 ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(2)若函数 在
在 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围.
(本小题13分)如图,在四棱锥 中,
中,
底面 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面 ,
, ,
, 是
是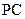 的中点,作
的中点,作 ⊥
⊥ 交
交 于点
于点 .
.
(1)证明: ∥平面
∥平面 ;
;
(2)证明: ⊥平面
⊥平面 .
.