函数
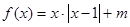
(1)设函数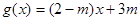 ,若方程
,若方程 在
在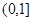 上有且仅一个实根,求实数
上有且仅一个实根,求实数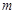 的取值范围;
的取值范围;
(2)当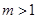 时,求函数
时,求函数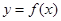 在
在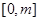 上的最大值.
上的最大值.
在等差数列{an}中,a1+a3=8,且a4为a2和a9的等比中项,求数列{an}的首项、公差及前n项和.
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-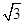 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
已知函数f(x)=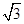 asin x+bcos
asin x+bcos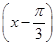 的图象经过点
的图象经过点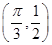 ,
,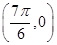 .
.
(1)求实数a,b的值;
(2)求函数f(2x)的周期及单调增区间.
已知函数f(x)=ax2-(a+2)x+ln x.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.