在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点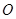 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线 的方程为
的方程为 .
.
(1)求曲线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(2)设曲线 和曲线
和曲线 的交点
的交点 、
、 ,求
,求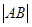 .
.
如图,点 是以线段
是以线段 为直径的圆
为直径的圆 上一点,
上一点,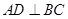 于点
于点 ,过点
,过点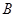 作圆
作圆 的切线,与
的切线,与 的延长线交于点
的延长线交于点 ,点
,点 是
是 的中点,连结
的中点,连结 并延长与
并延长与 相交于点
相交于点 ,延长
,延长 与
与 的延长线相交于点
的延长线相交于点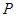 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: 是圆
是圆 的切线.
的切线.
已知圆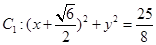 ,圆
,圆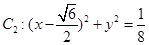 ,动圆
,动圆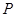 与已知两圆都外切.
与已知两圆都外切.
(1)求动圆的圆心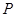 的轨迹
的轨迹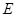 的方程(2)直线
的方程(2)直线 与点
与点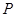 的轨迹
的轨迹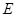 交于不同的两点
交于不同的两点 、
、 ,
,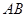 的中垂线与
的中垂线与 轴交于点
轴交于点 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.
已知函数 .
.
(Ⅰ)如果函数 在区间
在区间 上是单调函数,求
上是单调函数,求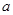 的取值范围;
的取值范围;
(Ⅱ)是否存在正实数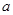 ,使得函数
,使得函数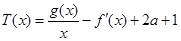 在区间
在区间 内有两个不同的零点(
内有两个不同的零点(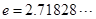 是自然对数的底数)?若存在,求出实数
是自然对数的底数)?若存在,求出实数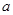 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
如图,平面 平面
平面 ,
, 是正方形,
是正方形, ,且
,且 ,
, 、
、 、
、 分别是线段
分别是线段 、
、 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求异面直线 、
、 所成角的余弦值.
所成角的余弦值.