为了预防流感，某学校对教室用药熏消毒法进行消毒.已知药物释放过程中，室内每立方米空气中的含药量
毫克）与时间
（小时）成正比；药物释放完毕后，与
的函数关系式为
（
为常数），如图所示，根据图中提供的信息，回答下列问题：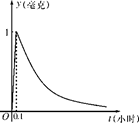
（1）求从药物释放开始，每立方米空气中的含药量（毫克）与时间（小时）之间的函数关系式;
（2）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室.那从药物释放开始，至少需要经过多少小时后，学生才能回到教室？
本题满分12分）已知：等差数列{
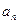}中，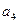
=14，前10项和
.
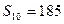（Ⅰ）求；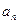
（Ⅱ）将{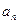}中的第2项，第4项，…，第
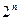项按
原来的顺序排成一个新数列，求此数列的前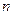
项和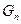
.
（本小题满分12）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且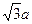
=2csinA
(Ⅰ)确定角C的大小：
（Ⅱ）若c＝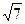
,且△ABC的面积为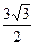
,求a＋b的值。
（本小题满分12分）
等比数列{
}的前n 项和为
，已知
,
,
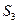成等差数列
（1）求{}的公比q；（2）求
－
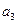＝3，求
解关于x的不等式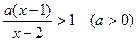
（本小题满分10分）选修4—5：不等式选讲
设函数f（x）＝｜2x－1｜＋｜x＋2｜．
（1）解不等式f（x）>3；
（2）若关于x的不等式f（x）≤｜2a－1｜的解集不是空集，试求a的取值范围．