某校课外兴趣小组的学生为了给学校边的一口被污染的池塘治污,他们通过实验后决定在池塘中投放一种能与水中的污染物质发生化学反应的药剂.已知每投放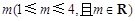 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度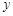 (克/升)随着时间
(克/升)随着时间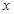 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为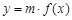 ,其中
,其中 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?
(Ⅱ)若第一次投放2个单位的药剂,6天后再投放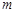 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求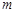 的最小值.
的最小值.
(本小题满分12分)已知函数f(x)=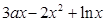 ,
, 为常数。
为常数。
(I)当 =1时,求f(x)的单调区间;
=1时,求f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求 的取值范围。
的取值范围。
(本小题满分12分)如图,在四棱锥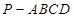 中,侧面
中,侧面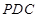 是边长为2的正三角形,且与底面垂直;底面
是边长为2的正三角形,且与底面垂直;底面 是菱形,
是菱形, ,
, 为
为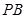 的中点.
的中点.
(1)求四棱锥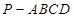 的体积;
的体积;
(2)求证: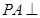 平面
平面 .
.
(本小题满分12分)已知等差数列{an}的前n项和为Sn,且a3=5,S15="225."
(1)求数列{an}的通项an;
(2)设bn= +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn.
(本小题满分12分)在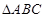 中,角
中,角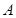 为锐角,记角
为锐角,记角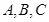 所对的边分别为
所对的边分别为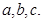 设向量
设向量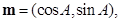
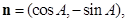 且
且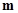 与
与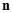 的夹角为
的夹角为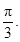
(1)求 的值及角
的值及角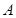 的大小;
的大小;
(2)若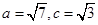 ,求
,求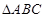 的面积
的面积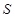 .
.
(本小题满分12分)已知函数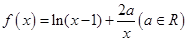 ,
,
(Ⅰ) 若a =1,求函数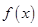 的图像在点
的图像在点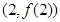 处的切线方程;
处的切线方程;
(Ⅱ)求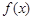 的单调区间;
的单调区间;
(Ⅲ)如果当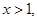 且
且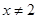 时,
时,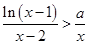 恒成立,求实数
恒成立,求实数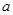 的取值范围。
的取值范围。