已知动点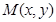 到定点
到定点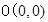 与到定点
与到定点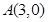 的距离之比为
的距离之比为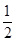 .
.
(1)求动点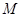 的轨迹C的方程,并指明曲线C的轨迹;
的轨迹C的方程,并指明曲线C的轨迹;
(2)设直线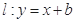 ,若曲线C上恰有三个点到直线
,若曲线C上恰有三个点到直线 的距离为1,求实数
的距离为1,求实数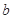 的值。
的值。
(本小题满分14分)
已知△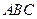 中,AB="AC," D是△
中,AB="AC," D是△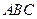 外接圆劣弧
外接圆劣弧 上的点(不与点A,C重合),延长BD至E。
上的点(不与点A,C重合),延长BD至E。
(1)求证:AD的延长线平分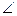 CDE;
CDE;
(2)若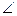 BAC=
BAC=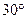 ,
, ABC中BC边上的高为2+
ABC中BC边上的高为2+ ,求△
,求△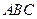 外接圆的面积。
外接圆的面积。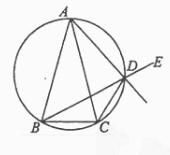
(本小题满分12分)某加工厂需要定期购买原材料,已知每公斤材料的价格为1.5元,每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(1)设该厂每 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在 天内总的保管费用
天内总的保管费用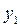 关于
关于 的函数关系式;
的函数关系式;
(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用 最少,并求出这个最少(小)值.
最少,并求出这个最少(小)值.
(本小题满分13分)
设函数 的定义域为R,当
的定义域为R,当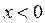 时,
时, ,且对任意的实数
,且对任意的实数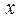 ,
, ,有
,有
(1)求 ; (2)试判断函数
; (2)试判断函数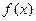 在
在 上是否存在最大值,若存在,求出该最大值,若不存在说明理由;
上是否存在最大值,若存在,求出该最大值,若不存在说明理由;
(3)设数列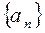 各项都是正数,且满足
各项都是正数,且满足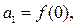
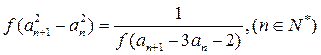 ,又设
,又设 ,
,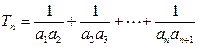 ,试比较
,试比较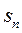 与
与  的大小.
的大小.
已知ΔABC的三个内角A、B.C满足 ,其中
,其中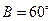 ,且
,且 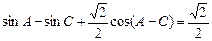 。
。
(1)求 、
、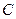 的大小;
的大小;
(2)求函数 在区间
在区间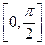 上的最大值与最小值。
上的最大值与最小值。
(本小题满分12分)
已知直线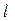 与函数
与函数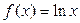 的图象相切于点(1,0),且
的图象相切于点(1,0),且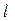 与函数
与函数 的图象也相切。
的图象也相切。
(1)求直线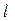 的方程及
的方程及 的值;
的值;
(2)若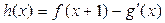 ,求函数
,求函数 的最大值.
的最大值.