已知向量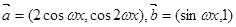
(
), 
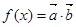,且
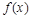的周期为
．
(1)求f(
)的值；
(2)写出f(x)在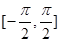
上的单调递增区间．
在
中,角
、
、
所对的边分别是
、
、
,向量
,且
与
共线．
（Ⅰ）求角的大小;
（Ⅱ）设
,求
的最大值及此时角的大小．
如图，在三棱锥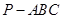
中，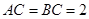
，
，
，
．
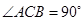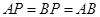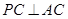（Ⅰ）求证：
；
（Ⅱ）求点
到平面
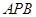的距离．
（本小题10分）第（1）小题5分，第（2）题8分
（1）已知直线
过点
且与直线
垂直，求直线的方程．
（2）已知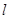直线
经过直线
与直线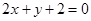
的交点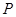
，且平行于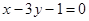直线
．求直线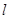与两坐标轴围成的三角形的面积；
（本小题满分13分）如图，已知
平面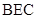
，
，
，
，
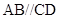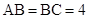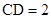为等边三角形．
（Ⅰ）求证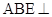：平面
平面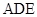
；
（Ⅱ）求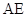
与平面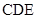
所成角的正弦值．
（本小题满分13分）已知在
中，
，
，
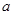分别是角
，
，
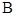的对边，且满足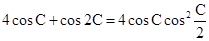
．
（Ⅰ）求角的大小；
（Ⅱ）若点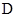
为边
的中点，求面积的最大值．