如图,在三棱锥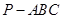 中,
中,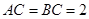 ,
,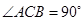 ,
,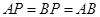 ,
,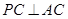 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求点 到平面
到平面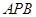 的距离.
的距离.
某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:
| 请假次数 |
 |
 |
 |
 |
| 人数 |
 |
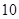 |
 |
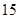 |
根据上表信息解答以下问题:
(1)从该小学任选两名教职工,用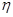 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数 在区间
在区间 上有且只有一个零点”为事件
上有且只有一个零点”为事件 ,求事件
,求事件 发生的概率
发生的概率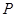 ;
;
(2)从该小学任选两名职工,用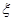 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量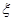 的分布列及数学期望
的分布列及数学期望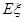 .
.
设函数f(x)=sin(ωx+ ),其中ω>0,|
),其中ω>0,| |<
|<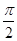 ,若cos
,若cos cos
cos -sin
-sin sin
sin =0,且图象的一条对称轴离一个对称中心的最近距离是
=0,且图象的一条对称轴离一个对称中心的最近距离是 .
.
(1)求函数f(x)的解析式;
(2)若A,B,C是△ABC的三个内角,且f(A)=-1,求sinB+sinC的取值范围.
已知函数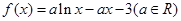 .
.
(Ⅰ)若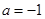 ,求函数
,求函数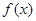 的单调区间;
的单调区间;
(Ⅱ)若函数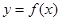 的图象在点(2,f(2))处的切线的倾斜角为
的图象在点(2,f(2))处的切线的倾斜角为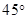 ,对于任意的
,对于任意的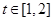 ,函数
,函数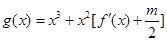
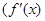 是
是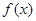 的导函数)在区间
的导函数)在区间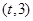 上总不是单调函数,求
上总不是单调函数,求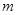 的取值范围;
的取值范围;
(Ⅲ)求证: .
.
已知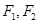 是椭圆
是椭圆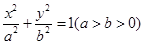 的左、右焦点,
的左、右焦点,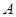 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点 也在椭圆上,且满足
也在椭圆上,且满足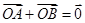 (
( 是坐标原点),
是坐标原点),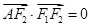 ,若椭圆的离心率为
,若椭圆的离心率为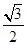 .
.
(1)若 的面积等于
的面积等于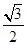 ,求椭圆的方程;
,求椭圆的方程;
(2)设直线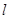 与(1)中的椭圆相交于不同的两点
与(1)中的椭圆相交于不同的两点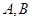 ,已知点
,已知点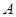 的坐标为(
的坐标为( ),点
),点 在线段
在线段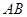 的垂直平分线上,且
的垂直平分线上,且 ,求
,求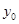 的值.
的值.
已知数列{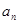 }的前n项和
}的前n项和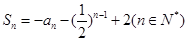 ,数列{
,数列{ }满足
}满足 =
=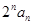 .
.
(I)求证:数列{ }是等差数列,并求数列{
}是等差数列,并求数列{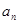 }的通项公式;
}的通项公式;
(Ⅱ)设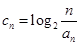 ,数列
,数列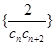 的前
的前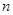 项和为
项和为 ,求满足
,求满足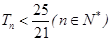 的
的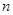 的最大值.
的最大值.