已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC= AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
在数列 中,已知
中,已知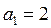 ,
,
(1)试写出 ,并求数列
,并求数列 的通项公式
的通项公式 ;
;
设
 ,求数列
,求数列 的前
的前 项和
项和 。
。
在三角形ABC中,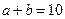 ,
,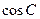 是方程
是方程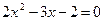 的一个根,求:
的一个根,求:
(1)角C的度数;
(2)三角形ABC周长的最小值。
设函数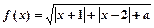 .
.
(I)当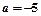 时,求函数
时,求函数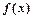 的定义域;
的定义域;
(II)若函数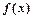 的定义域为
的定义域为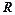 ,试求
,试求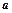 的取值范围
的取值范围
设函数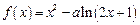 (
(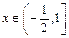 ,
,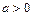 ).
).
(I)若函数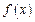 在其定义域内是减函数,求
在其定义域内是减函数,求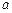 的取值范围;
的取值范围;
(II)函数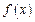 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时 的值,并证明你的结论.
的值,并证明你的结论.
已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
(I)求f(x)的解析式;
(II)已知k的取值范围为[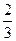 ,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.