(本小题满分13分)如图,已知 平面
平面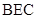 ,
,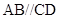 ,
,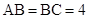 ,
,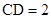 ,
, 为等边三角形.
为等边三角形.
(Ⅰ)求证:平面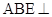 平面
平面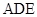 ;
;
(Ⅱ)求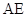 与平面
与平面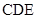 所成角的正弦值.
所成角的正弦值.
(本小题共14分)
已知函数 在
在 与
与 处都取得极值.
处都取得极值.
(Ⅰ)求 的值及函数
的值及函数 的单调区间;
的单调区间;
(Ⅱ)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题共13分)
在平面直角坐标系 中,平面区域
中,平面区域 中的点的坐标
中的点的坐标 满足
满足 ,从区域
,从区域 中随机取点
中随机取点 .
.
(Ⅰ)若 ,
, ,求点
,求点 位于第四象限的概率;
位于第四象限的概率;
(Ⅱ)已知直线 与圆
与圆 相交所截得的弦长为
相交所截得的弦长为 ,
,
求 的概率.
的概率.
(本小题共14分)
正方体 的棱长为
的棱长为 ,
, 是
是 与
与 的交点,
的交点, 为
为 的中点.
的中点.
(Ⅰ)求证:直线 ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
|
如图,在平面直角坐标系 中,以
中,以 轴为始边作两个锐角
轴为始边作两个锐角 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于 两点.已知
两点.已知 的横坐标分别为
的横坐标分别为 .
.
 的值;
的值;
 的值.
的值.

(满分14分)
已知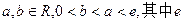 是自然对数的底数。
是自然对数的底数。
(1)试猜想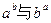 的大小关系;
的大小关系;
(2)证明你的结论。