过双曲线x2-y2=1上一点M作直线x+y=2的垂线,垂足为N,求线段MN的中点P的轨迹方程.
已知函数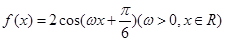 的最小正周期为
的最小正周期为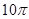 .
.
(1)求函数 的对称轴方程;
的对称轴方程;
(2)设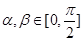 ,
,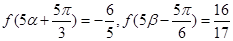 ,求
,求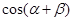 的值.
的值.
设集合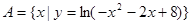 ,集合
,集合 ,集合C为不等式
,集合C为不等式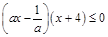 的解集.
的解集.
(1)求 ;
;
(2)若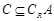 ,求a的取值范围.
,求a的取值范围.
甲、乙两人玩转盘游戏,该游戏规则是这样的:一个质地均匀的标有12等分数字格的转盘(如图),甲、乙两人各转转盘一次,转盘停止时指针所指的数字为该人的得分.(假设指针不能指向分界线)现甲先转,乙后转,求下列事件发生的概率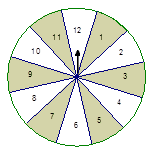
(1)甲得分超过7分的概率.
(2)甲得7分,且乙得10分的概率
(3)甲得5分且获胜的概率.
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程 ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.