某校从高一年级期末考试的学生中抽出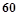 名学生,其成绩(均为整数)的频率分布直方图如图所示:
名学生,其成绩(均为整数)的频率分布直方图如图所示:
(Ⅰ)估计这次考试的及格率(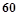 分及以上为及格)和平均分;
分及以上为及格)和平均分;
(Ⅱ)从成绩是 分以上(包括
分以上(包括 分)的学生中选两人,求他们在同一分数段的概率.
分)的学生中选两人,求他们在同一分数段的概率.
(有难度哦)给定有限单调递增数列
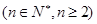 且
且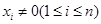 ,定义集合
,定义集合 且
且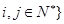 .若对任意点
.若对任意点 ,存在点
,存在点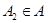 使得
使得 (
( 为坐标原点),则称数列
为坐标原点),则称数列 具有性质
具有性质 .
.
(Ⅰ)判断数列 :
: 和数列
和数列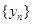 :
: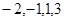 是否具有性质
是否具有性质 ,简述理由.
,简述理由.
(Ⅱ)若数列 具有性质
具有性质 ,求证:
,求证:
①数列 中一定存在两项
中一定存在两项 使得
使得 ;
;
②若 ,
,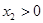 且
且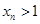 ,则
,则 .
.
已知数列{an}的前n项和Sn满足Sn+1=kSn+2(n∈N*),且a1=2,a2=1.
(1)求k的值和Sn的表达式;
(2)是否存在正整数m,n,使得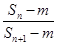 <
<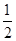 成立?若存在,求出这样的正整数;若不存在,请说明理由.
成立?若存在,求出这样的正整数;若不存在,请说明理由.
设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有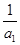 +
+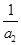 +…+
+…+ <
< .
.
设数列{an}满足a1+3a2+32a3+…+3n-1an= ,n∈N*.
,n∈N*.
(1)求数列{an}的通项;
(2)设bn=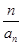 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足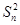 =an
=an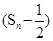 .
.
(1)求Sn的表达式;
(2)设bn=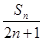 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.