已知数列{an}的前n项和Sn满足Sn+1=kSn+2(n∈N*),且a1=2,a2=1.
(1)求k的值和Sn的表达式;
(2)是否存在正整数m,n,使得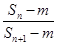 <
<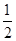 成立?若存在,求出这样的正整数;若不存在,请说明理由.
成立?若存在,求出这样的正整数;若不存在,请说明理由.
已知数列 满足
满足 ,
, ;数列
;数列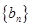 满足
满足 ,
,  .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)求数列 、
、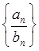 的前
的前 项和
项和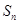 ,
, .
.
设函数 .
.
(1)求函数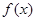 的最小正周期;
的最小正周期;
(2)若 ,且
,且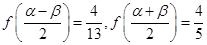 ,求
,求 的值.
的值.
锐角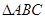 中,
中,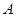 、
、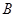 、
、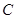 分别为
分别为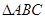 的三边
的三边 、
、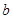 、
、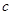 所对的角,
所对的角,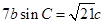 ,
, 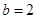 ,
, .
.
(1)求角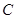 ;
;
(2)求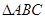 的面积
的面积 .
.
在四边形 中,
中,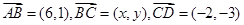 .
.
(1)若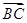 ∥
∥ ,试求
,试求 与
与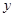 满足的关系
满足的关系
(2)若满足(1)同时又有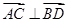 ,求
,求 、
、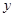 的值.
的值.
国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校期间所需的学费、住宿费及生活费。每一年度申请总额不超过6000元。某大学2012届毕业生凌霄在本科期间共申请了24000元助学贷款,并承诺毕业后3年(按36个月计)内还清。签约单位提供的工资标准为第一年内每月1500元,第13个月开始每月工资比前一个月增加5%直到4000元。凌霄同学计划前12个月每月还款500元,第13个月开始每月还款比前一个月多 元.
元.
(1)若凌霄同学恰好在第36个月(即毕业后3年)还清贷款,求 值;
值;
(2)当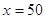 时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?
时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?
(参考数据: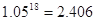 ,
,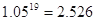 ,
,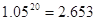 ,
,  )
)