[2014高考真题] 在平面直角坐标系xOy中,点M到点F(1,0)的距离比它到y轴的距离多1.记点M的轨迹为C.
(1)求轨迹C的方程;
(2)(注意分类讨论哦)设斜率为k的直线l过定点P(-2,1),求直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.
(本小题满分12分)为了解决西部地区某希望小学的师生饮水问题,中原名校联谊会准备援建一个无盖的圆柱形蓄水池(不计厚度),设该蓄水池底面半径为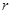 米,高
米,高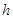 米,体积为
米,体积为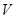 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为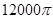 元(
元(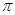 为圆周率).
为圆周率).
(1)将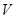 表示成
表示成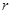 的函数
的函数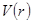 ,并求函数的定义域;
,并求函数的定义域;
(2)讨论函数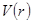 的单调性,并确定
的单调性,并确定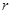 和
和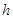 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
(本小题满分12分)在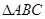 中,角
中,角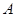 ,
,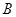 ,
,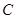 的对边分别为
的对边分别为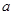 ,
,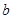 ,
,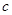 ,已知向量
,已知向量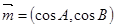 ,
,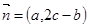 ,且
,且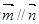 .
.
(1)求角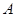 的大小;
的大小;
(2)若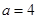 ,求
,求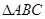 面积的最大值.
面积的最大值.
(本小题满分12分)已知二次函数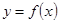 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为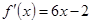 .数列
.数列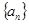 的前
的前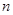 项和为
项和为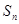 ,点
,点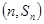
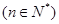 均在函数
均在函数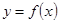 的图象上.
的图象上.
(1)求数列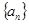 的通项公式;
的通项公式;
(2)设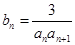 ,
,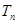 是数列
是数列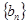 的前
的前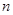 项和,求使得
项和,求使得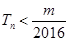 对所有
对所有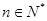 都成立的最小正整数
都成立的最小正整数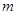 .
.
(本小题满分10分)设命题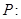 函数
函数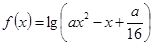 的定义域为
的定义域为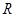 ;命题
;命题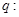 不等式
不等式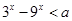 对一切正实数
对一切正实数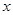 均成立..
均成立..
(1)如果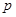 是真命题,求实数
是真命题,求实数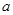 的取值范围;
的取值范围;
(2)如果命题“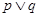 ”为真命题,且“
”为真命题,且“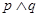 ”为假命题,求实数
”为假命题,求实数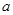 的取值范围.
的取值范围.
(本题10分) 设 是偶函数,且当
是偶函数,且当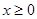 时,
时,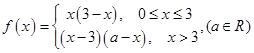 .
.
(1)当 时,求
时,求 的解析式;
的解析式;
(2)设函数 在区间
在区间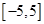 上的最大值为
上的最大值为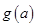 ,试求
,试求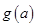 的表达式.
的表达式.