已知动圆P过点F 且与直线y=
且与直线y=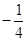 相切.
相切.
(1)求圆心P的轨迹C的方程;
(2)过点F作一条直线交轨迹C于A,B两点,轨迹C在A,B两点处的切线相交于N,M为线段AB的中点,求证:MN⊥x轴.
已知圆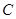 :
: ,点
,点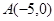 ,直线
,直线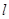 :
: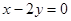 .
.
⑴求与圆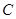 相切,且与直线
相切,且与直线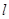 垂直的直线方程;
垂直的直线方程;
⑵若在直线 上(
上( 为坐标原点)存在定点
为坐标原点)存在定点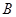 (不同于点
(不同于点 ),满足:对于圆
),满足:对于圆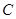 上任意一点
上任意一点 ,都有
,都有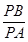 为一常数,求所有满足条件的点
为一常数,求所有满足条件的点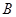 的坐标.
的坐标.
直线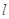 经过点
经过点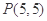 ,其斜率为
,其斜率为 ,直线
,直线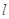 与圆
与圆 相交,交点分别为
相交,交点分别为 .
.
(1)若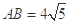 ,求
,求 的值;
的值;
(2)若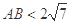 ,求
,求 的取值范围;
的取值范围;
(3)若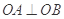 (
( 为坐标原点),求
为坐标原点),求 的值.
的值.
直线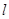 过点
过点 且斜率为
且斜率为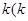 >
>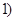 ,将直线
,将直线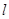 绕
绕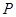 点按逆时针方向旋转45°得直线
点按逆时针方向旋转45°得直线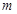 ,若直线
,若直线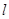 和
和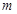 分别与
分别与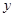 轴交于
轴交于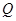 ,
,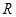 两点.(1)用
两点.(1)用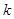 表示直线
表示直线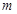 的斜率;(2)当
的斜率;(2)当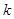 为何值时,
为何值时,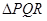 的面积最小?并求出面积最小时直线
的面积最小?并求出面积最小时直线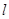 的方程.
的方程.
已知平面直角坐标系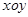 中O是坐标原点,
中O是坐标原点,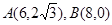 ,圆
,圆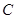 是
是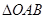 的外接圆,过点(2,6)的直线为
的外接圆,过点(2,6)的直线为 。
。
(1)求圆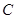 的方程;
的方程;
(2)若 与圆相切,求切线方程;
与圆相切,求切线方程;
(3)若 被圆所截得的弦长为
被圆所截得的弦长为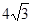 ,求直线
,求直线 的方程。
的方程。
已知直线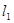 :
: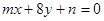 与直线
与直线 :
: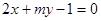 互相平行,经过点
互相平行,经过点 的直线
的直线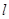 与
与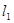 ,
, 垂直,且被
垂直,且被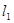 ,
, 截得的线段长为
截得的线段长为 ,试求直线
,试求直线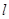 的方程.
的方程.