如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
先化简,再求值: ,其中 .
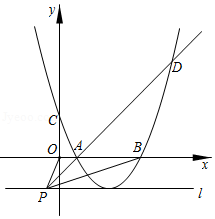
如图所示,二次函数 的图象(记为抛物线 与 轴交于点 ,与 轴分别交于点 、 ,点 、 的横坐标分别记为 , ,且 .
(1)若 , ,且过点 ,求该二次函数的表达式;
(2)若关于 的一元二次方程 的判别式△ .求证:当 时,二次函数 的图象与 轴没有交点.
(3)若 ,点 的坐标为 , ,过点 作直线 垂直于 轴,且抛物线的 的顶点在直线 上,连接 、 、 , 的延长线与抛物线 交于点 ,若 ,求 的最小值.
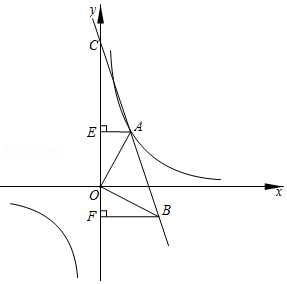
如图所示, 的顶点 在反比例函数 的图象上,直线 交 轴于点 ,且点 的纵坐标为5,过点 、 分别作 轴的垂线 、 ,垂足分别为点 、 ,且 .
(1)若点 为线段 的中点,求 的值;
(2)若 为等腰直角三角形, ,其面积小于3.
①求证: ;
②把 称为 , , , 两点间的“ 距离”,记为 ,求 , , 的值.
是 的直径,点 是 上一点,连接 、 ,直线 过点 ,满足 .
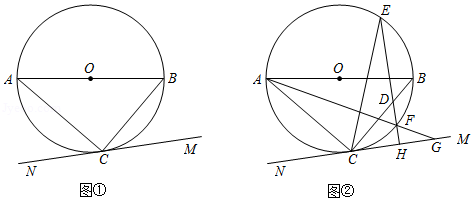
(1)如图①,求证:直线 是 的切线;
(2)如图②,点 在线段 上,过点 作 于点 ,直线 交 于点 、 ,连接 并延长交直线 于点 ,连接 ,且 ,若 的半径为1, ,求 的值.
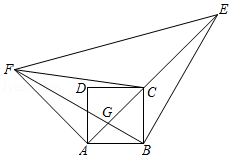
如图所示, 的顶点 在正方形 对角线 的延长线上, 与 交于点 ,连接 、 ,满足 .
(1)求证: .
(2)若正方形 的边长为1, ,求 的值.