已知：如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，-优题课

某中学开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人．

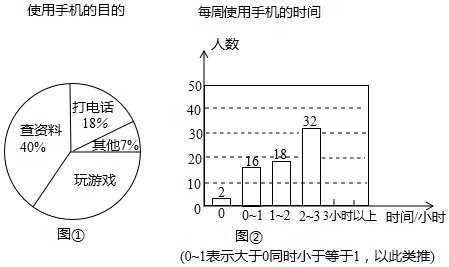
请你根据以上信息解答下列问题：

（1）在扇形统计图中，“玩游戏”对应的圆心角度数是　度；

（2）补全条形统计图；

（3）该校共有学生1200人，估计每周使用手机时间在2小时以上（不含2小时）的人数．

小华和小军做摸球游戏： $A$ 袋装有编号为1，2，3的三个小球， $B$ 袋装有编号为4，5，6的三个小球，两袋中的所有小球除编号外都相同．从两个袋子中分别随机摸出一个小球，若 $B$ 袋摸出小球的编号与 $A$ 袋摸出小球的编号之差为偶数，则小华胜，否则小军胜．这个游戏对双方公平吗？请说明理由．

已知：四边形 $ABCD$ ．

求作：点 $P$ ，使 $∠ PCB = ∠ B$ ，且点 $P$ 到边 $AD$ 和 $CD$ 的距离相等．

如图，抛物线 $y = a x^{2} + bx - 3$ 经过点 $A (2, - 3)$ ，与 $x$ 轴负半轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，且 $OC = 3 OB$ ．

（1）求抛物线的解析式；

（2）点 $D$ 在 $y$ 轴上，且 $∠ BDO = ∠ BAC$ ，求点 $D$ 的坐标；

（3）点 $M$ 在抛物线上，点 $N$ 在抛物线的对称轴上，是否存在以点 $A$ ， $B$ ， $M$ ， $N$ 为顶点的四边形是平行四边形？若存在，求出所有符合条件的点 $M$ 的坐标；若不存在，请说明理由．

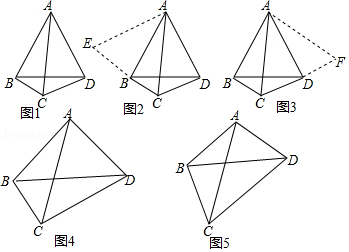
数学课上，张老师出示了问题：如图1， $AC$ ， $BD$ 是四边形 $ABCD$ 的对角线，若 $∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = 60 °$ ，则线段 $BC$ ， $CD$ ， $AC$ 三者之间有何等量关系？

经过思考，小明展示了一种正确的思路：如图2，延长 $CB$ 到 $E$ ，使 $BE = CD$ ，连接 $AE$ ，证得 $ΔABE ≅ ΔADC$ ，从而容易证明 $ΔACE$ 是等边三角形，故 $AC = CE$ ，所以 $AC = BC + CD$ ．

小亮展示了另一种正确的思路：如图3，将 $ΔABC$ 绕着点 $A$ 逆时针旋转 $60 °$ ，使 $AB$ 与 $AD$ 重合，从而容易证明 $ΔACF$ 是等边三角形，故 $AC = CF$ ，所以 $AC = BC + CD$ ．

在此基础上，同学们作了进一步的研究：

（1）小颖提出：如图4，如果把“ $∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = 60 °$ ”改为“ $∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = 45 °$ ”，其它条件不变，那么线段 $BC$ ， $CD$ ， $AC$ 三者之间有何等量关系？针对小颖提出的问题，请你写出结论，并给出证明．

（2）小华提出：如图5，如果把“ $∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = 60 °$ ”改为“ $∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = α$ ”，其它条件不变，那么线段 $BC$ ， $CD$ ， $AC$ 三者之间有何等量关系？针对小华提出的问题，请你写出结论，不用证明．