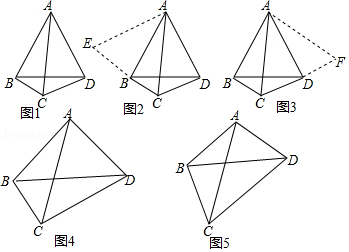
数学课上，张老师出示了问题：如图1， $\mathit{AC}$， $\mathit{BD}$是四边形 $\mathit{ABCD}$的对角线，若 $\angle \mathit{ACB}=\angle \mathit{ACD}=\angle \mathit{ABD}=\angle \mathit{ADB}=60°$，则线段 $\mathit{BC}$， $\mathit{CD}$， $\mathit{AC}$三者之间有何等量关系？

经过思考，小明展示了一种正确的思路：如图2，延长 $\mathit{CB}$到 $E$，使 $\mathit{BE}=\mathit{CD}$，连接 $\mathit{AE}$，证得 $\mathit{\Delta ABE}\cong \mathit{\Delta ADC}$，从而容易证明 $\mathit{\Delta ACE}$是等边三角形，故 $\mathit{AC}=\mathit{CE}$，所以 $\mathit{AC}=\mathit{BC}+\mathit{CD}$．

小亮展示了另一种正确的思路：如图3，将 $\mathit{\Delta ABC}$绕着点 $A$逆时针旋转 $60°$，使 $\mathit{AB}$与 $\mathit{AD}$重合，从而容易证明 $\mathit{\Delta ACF}$是等边三角形，故 $\mathit{AC}=\mathit{CF}$，所以 $\mathit{AC}=\mathit{BC}+\mathit{CD}$．

在此基础上，同学们作了进一步的研究：

（1）小颖提出：如图4，如果把“ $\angle \mathit{ACB}=\angle \mathit{ACD}=\angle \mathit{ABD}=\angle \mathit{ADB}=60°$”改为“ $\angle \mathit{ACB}=\angle \mathit{ACD}=\angle \mathit{ABD}=\angle \mathit{ADB}=45°$”，其它条件不变，那么线段 $\mathit{BC}$， $\mathit{CD}$， $\mathit{AC}$三者之间有何等量关系？针对小颖提出的问题，请你写出结论，并给出证明．

（2）小华提出：如图5，如果把“ $\angle \mathit{ACB}=\angle \mathit{ACD}=\angle \mathit{ABD}=\angle \mathit{ADB}=60°$”改为“ $\angle \mathit{ACB}=\angle \mathit{ACD}=\angle \mathit{ABD}=\angle \mathit{ADB}=\alpha$”，其它条件不变，那么线段 $\mathit{BC}$， $\mathit{CD}$， $\mathit{AC}$三者之间有何等量关系？针对小华提出的问题，请你写出结论，不用证明．

科目 数学   题型 解答题   难度 中等

知识点： 几何变换综合题 全等三角形的判定与性质 等腰三角形的判定与性质