某玩具批发商销售每件进价为40元的玩具,市场调查发现,若以每件50元的价格销售,平均每天销售90件,单价每提高1元,平均每天就少销售3件.
(1)平均每天的销售量y(件)与销售价x(元/件)之间的函数关系式为 ;
(2)求该批发商平均每天的销售利润W(元)与销售价x(元/件)之间的函数关系式;
(3)物价部门规定每件售价不得高于55元,当每件玩具的销售价为多少元时,可以获得最大利润?最大利润是多少元?
某温室大棚用花盆培育花苗,经过实验发现,每盆的盈利与每盆的株数构成一定的关系:每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加一株,平均单株盈利就减少0.5元。
(1)如果每盆花苗(假设原来花盆中有3株花苗)增加a株,则每盆花苗有株,平均单株盈利为元;
(2)要使每盆的盈利达到10元,每盆应该植入多少株?
如图所示,⊙O 的半径是4,PA、PB分别与⊙O相切于点A、点B,若PA与PB之间的夹角∠APB=60°, 
(1)若点C是圆上的一点,试求∠ACB的大小;
(2)求△ABP的周长
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AF⊥BD,CE⊥BD,垂足分别为E、F;连结AE、CF,得四边形AFCE,试判断四边形AFCE是下列图形中的哪一种?①平行四边形;②菱形;③矩形;请证明你的结论.
(本小题满分10分)如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D。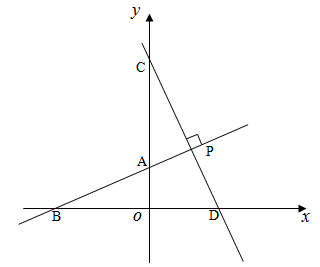
(1)求出点A、点B的坐标。
(2)请求出直线CD的解析式。
(3)若点M为坐标平面内任意一点,在直线AB上是否存在这样的点M,使以点B、D、M为顶点的三角形与△AOB相似,若存在,请直接写出点M的坐标;若不存在,请说明理由。
去年牡丹江管理局西瓜喜获丰收,瓜农老李收获的200吨西瓜计划采用批发和零售两种方式进行销售。经市场调查发现:批发销售每吨可获利200元,零售每吨可获利600元。
(1)若老李计划将这200吨西瓜批发销售x吨,其余零售,设所获总利润y元,试写出y与x之间的函数
关系式。(不必写出自变量的取值范围)
(2)如果老李决定将这200吨西瓜采取批发和零售两种销售方式,他预计获利不低于50000元,不高于52000元。请问共有几种销售方案?(批发和零售的吨数均为正整数)
(3)老李决定将(2)中获利的20﹪全部用来购进今年种植西瓜所需的A、B两种化肥,其中A种化肥每吨4000元,B种化肥每吨2000元(A、B两种化肥的吨数均为正整数)。请直接写出老李有哪几种购进方案.