如图，斜率为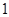
的直线过抛物线
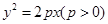的焦点，与抛物线交于两点A、B， M为抛物线弧AB上的动点．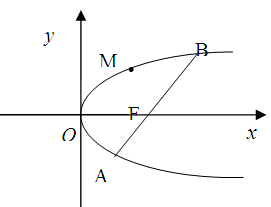
(Ⅰ)若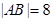
，求抛物线的方程；
(Ⅱ)求△ABM面积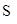
的最大值．
已知数列
的前
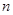项和为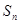
，
．
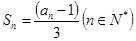（Ⅰ）求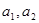
；
（Ⅱ）求证：数列是等比数列．
在锐角△ABC中，a、b、c分别为∠A、∠B、∠C所对的边，且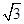
a＝2csinA.
(1)确定∠C的大小；
(2)若c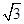＝，求△ABC周长的取值范围．
已知等差数列{an}的前n项的和记为Sn．如果a4＝－12，a8＝－4．
(1)求数列{an}的通项公式；
(2)求Sn的最小值及其相应的n的值；
△ABC中，BC＝7，AB＝3，且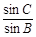
＝
．
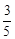(1)求AC的长；
(2)求∠A的大小．
设等差数列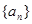
的前ｎ项的和为S n ,且S 4 =－62, S 6 =－75,求：
（1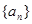）的通项公式a n及前ｎ项的和S n；
（2）|a 1 |+|a 2 |+|a 3 |+……+|a 14 |.