已知偶函数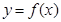 满足:当
满足:当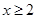 时,
时,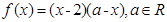 ,当
,当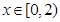 时,
时,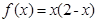 .
.
(Ⅰ)求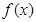 表达式;
表达式;
(Ⅱ)若直线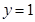 与函数
与函数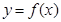 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数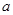 的取值范围;
的取值范围;
(Ⅲ)试讨论当实数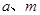 满足什么条件时,直线
满足什么条件时,直线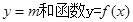 的图像恰有
的图像恰有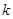 个公共点
个公共点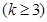 ,且这
,且这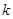 个公共点均匀分布在直线
个公共点均匀分布在直线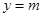 上.(不要求过程)
上.(不要求过程)
已知椭圆焦点是 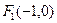 和
和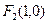 ,离心率
,离心率 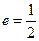
(1)求椭圆的标准方程;
(2)设点 在这个椭圆上,且
在这个椭圆上,且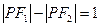 ,求
,求 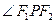 的余弦值.
的余弦值.
已知某物体的位移 (米)与时间
(米)与时间 (秒)的关系是
(秒)的关系是 ,
,
(1)求 秒到
秒到 秒的平均速度;
秒的平均速度;
(2)求此物体在 秒的瞬时速度.
秒的瞬时速度.
(本小题13分)
已知椭圆的焦点在 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线 ,交椭圆于A、B两点.
,交椭圆于A、B两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点M(m,0)是线段OF上的一个动点,且 ,求
,求 取值范围;
取值范围;
(Ⅲ)设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C、B、N 三点共线?若存在,求出定点N的坐标,若不存在,请说明理由.
(本小题12分)
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B.
(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求直线BC与平面DEF所成角的余弦值;
(Ⅲ)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
(本小题15分)
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D ;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.