(本题9分)设函数 。
。
(1)求 的值;
的值;
(2)求 的最小值及
的最小值及 取最小值时
取最小值时 的集合;(3)求
的集合;(3)求 的单调递增区间。
的单调递增区间。
(本题8分)已知等差数列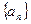 满足:
满足: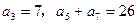 ,
,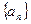 的前
的前 项和为
项和为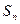 。
。
(1)求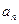 及
及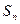 ;
;
(2)令 (其中
(其中 为常数,且
为常数,且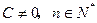 ),求证数列
),求证数列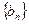 为等比数列。
为等比数列。
(本题8分)在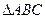 中,角
中,角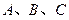 所对的边
所对的边 分别为
分别为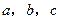 ,已知
,已知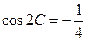 。
。
(1)求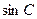 的值;
的值;
(2)当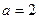 ,
,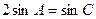 时,求
时,求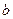 及
及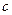 的长。
的长。
(本题9分)在平面直角坐标系 中,点
中,点 、
、 、
、 。
。
(1)求以线段 为邻边的平行四边形两条对角线的长;
为邻边的平行四边形两条对角线的长;
(2)当 为何值时,
为何值时, 与
与 垂直;
垂直;
(3)当 为何值时,
为何值时,
 与
与 平行,平行时它们是同向还是反向。
平行,平行时它们是同向还是反向。
(本题9分)甲袋中有3只白球、7只红球、1 5只黑球;乙袋中有10只白球、6只红球、9只黑球。
5只黑球;乙袋中有10只白球、6只红球、9只黑球。
(1)从甲袋中任取一球,求取到白球的概率;
(2)从两袋中各取一球,求两球颜色相同的概率;
(3)从两袋中各取一球,求两球颜色不同的概率。