设函数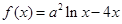 ,
,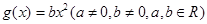 .
.
(1)当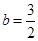 时,函数
时,函数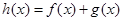 在
在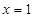 处有极小值,求函数
处有极小值,求函数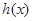 的单调递增区间;
的单调递增区间;
(2)若函数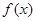 和
和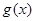 有相同的极大值,且函数
有相同的极大值,且函数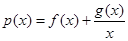 在区间
在区间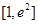 上的最大值为
上的最大值为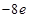 ,求实数
,求实数 的值(其中
的值(其中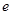 是自然对数的底数).
是自然对数的底数).
某校为了解高三开学数学考试的情况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.
(1)求直方图中x的值;
(2)试根据样本估计“该校高三学生期末数学考试成绩≥70”的
概率;
(3)试估计所抽取的数学成绩的平均数.
(1)已知不等式ax2一bx+1≥0的解集是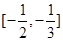 ,求不等式一x2+bx+a>0的解集;
,求不等式一x2+bx+a>0的解集;
(2)若不等式ax2+ 4x十a>1—2x2对任意x∈R均成立,求实数a的取值范围.
己知集合A="{x" |y=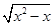 }, B={y|y=x2+x+l,x∈ R).
}, B={y|y=x2+x+l,x∈ R).
(1)求A,B;(2)求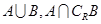 .
.
(本小题满分14分)
(1)已知ex≥ax +1,对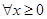 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)己知 ,0<x<m,求证f(x)<
,0<x<m,求证f(x)<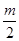 .
.
(本小题满分12分)己知函数f(x)= 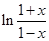
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求证:当x∈(0,1)时,f(x)>2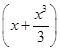
(3)设实数k使得f(x)>k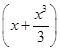 对x∈(0,1)恒成立,求k的最大值.
对x∈(0,1)恒成立,求k的最大值.