在 中,已知
中,已知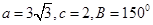 ,求边
,求边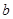 的长及
的长及 的面积.
的面积.
(本小题满分14分)在四边形 中,已知
中,已知 ,
, ,
, .
.
(1)若四边形 是矩形,求
是矩形,求 的值;
的值;
(2)若四边形 是平行四边形,且
是平行四边形,且 ,求
,求 与
与 夹角的余弦值.
夹角的余弦值.
已知函数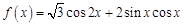 ,
,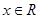 .
.
(1)求函数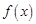 的最小正周期;
的最小正周期;
(2)求函数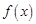 在区间
在区间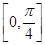 上的值域.
上的值域.
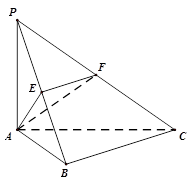
如图,在三棱锥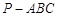 中,
中,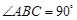 ,
,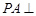 平面
平面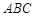 ,
,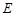 ,
,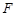 分别为
分别为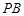 ,
, 的中点.
的中点.
(1)求证: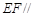 平面
平面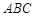 ;
;
(2)求证:平面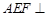 平面
平面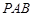 .
.
已知圆C过点P(1,1),且与圆M:(x+2)2+(x+2)2=r2(r>0)2关于直线x+y+2=0对称.
⑴求圆C的方程;
⑵设Q为圆C上的一个动点,求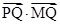 的最小值;
的最小值;
⑶过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2 000元.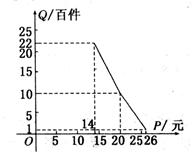
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?