如图,在平面直角坐标系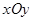 中,点
中,点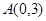 ,直线
,直线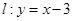 。设圆
。设圆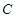 的半径为
的半径为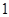 ,圆心在
,圆心在 上。
上。
(1)若圆心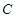 也在直线
也在直线 上,过点
上,过点 作圆
作圆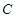 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆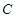 上存在点
上存在点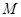 ,使
,使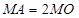 ,求圆心
,求圆心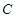 的横坐标
的横坐标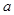 的取值范围。
的取值范围。
已知数列 和
和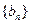 中,数列
中,数列 的前
的前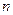 项和记为
项和记为 . 若点
. 若点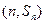 在函数
在函数 的图象上,点
的图象上,点 在函数
在函数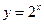 的图象上。
的图象上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列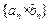 的前
的前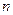 项和
项和
已知 ,函数
,函数 (
( R).
R).
(1)求 ; (2)求
; (2)求 的最小正周期和最大值;
的最小正周期和最大值;
(3)若 为锐角,且
为锐角,且 ,求
,求 的值
的值
已知直线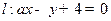 及圆
及圆
(1) 若直线l与圆C相切,求a的值;
(2) 若直线l与圆C相交于A,B两点,且弦AB的长为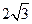 ,求a的值.
,求a的值.
从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下(单位:分):
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例.
在直角坐标系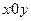 中,点
中,点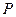 到两点
到两点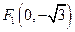 、
、 的距离之和等于4,设点
的距离之和等于4,设点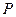 的轨迹为曲线
的轨迹为曲线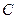 ,直线
,直线 与曲线
与曲线 交于
交于 、
、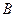 两点.
两点.
(1)求出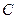 的方程;
的方程;
(2)若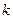 =1,求
=1,求 的面积;
的面积;
(3)若OA⊥OB,求实数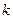 的值。
的值。